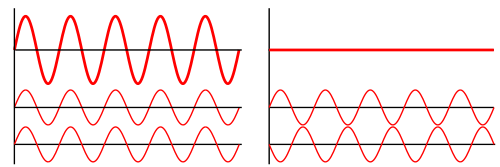
解释了回归均值效应，还需要搞清楚的是虽然事物大部分时间都有小幅的随机波动，但偶然也会出现较大的波动，即极好或者极差的状态，正如上图的B段状态，我们如何认定这个状态也是随机的，而不是异常呢，不能因为难以解释而不把过大的数据波动当做一种异常来看?

　　这个问题还是可以从物理学的角度开始解释，先看下波的叠加原理(Superposition Principle)：

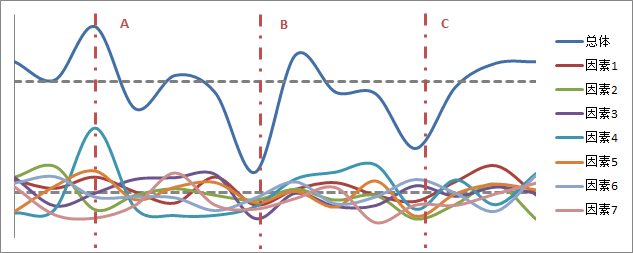
　　左图的下面2个波在叠加之后合成了更大的振幅，而右图的下面2个波相互干涉，合成后振幅消减为零。引申到数据变化的情境下，一般一个指标会受到多个因素的影响，比如网站的访问量会受多个渠道数据波动的影响，搜索引擎、外部链接、社交媒介、付费广告等这些外部渠道带来的流量总是在变化的，如下图：

　　当某个渠道的流量异常的时候，如A线所示，或者由于外界因素的影响，如春节或节假日所有渠道的流量都可能普遍下降，如B线所示，这些都可能导致总体访问量的异常，这些异常是可以解释的。C线中每个渠道的数据都未出现明显异常，但由于多个渠道的流量因为随机波动碰巧同时都到了一个较低的点，这个时候总体访问量也会出现明显低于正常水平的情况，于是就出现了“难以解释的异常”。

　　所以，这些“难以解释的异常”之谜可以揭晓了，当很多因素同时作用于某个指标的时候，即使所有的影响因素都没有出现显著的异常，指标数据仍然可能表现异常，虽然这个概率非常低，但确实会发生，这是因为多个因素共同作用下的叠加效应导致的，如果通过细分指标的影响因素没有发现明显的异常，那么不要试图为这个“难以解释的异常”寻找看上去可以解释的原因。

　　» 本文采用 BY-NC-SA 协议，转载请注明来源：网站数据分析 » 《难以解释的数据异常》

        原文：