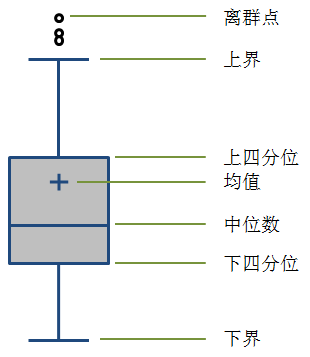
数据质量(Data Quality)是数据分析结论有效性和准确性的基础也是最重要的前提和保障。数据质量保证(Data Quality Assurance)是数据仓库架构中的重要环节，也是ETL的重要组成部分。

　　我们通常通过数据清洗(Data cleansing)来过滤脏数据，保证底层数据的有效性和准确性，数据清洗一般是数据进入数据仓库的前置环节，一般来说数据一旦进入数据仓库，那么必须保证这些数据都是有效的，上层的统计聚合都会以这批数据作为基础数据集，上层不会再去做任何的校验和过滤，同时使用稳定的底层基础数据集也是为了保证所有上层的汇总和多维聚合的结果是严格一致的。但当前我们在构建数据仓库的时候一般不会把所有的数据清洗步骤放在入库之前，一般会把部分数据清洗的工作放在入库以后来执行，主要由于数据仓库对数据处理方面有自身的优势，部分的清洗工作在仓库中进行会更加的简单高效，而且只要数据清洗发生在数据的统计和聚合之前，我们仍然可以保证使用的是清洗之后保留在数据仓库的最终“干净”的基础数据。

　　前段时间刚好跟同事讨论数据质量保证的问题，之前做数据仓库相关工作的时候也接触过相关的内容，所以这里准备系统地整理一下。之前构建数据仓库基于Oracle，所以选择的是Oracle提供的数据仓库构建工具——OWB(Oracle Warehouse Builder)，里面提供了比较完整的保证数据质量的操作流程，主要包括三块：

　　Data Profiling

　　Data Auditing

　　Data Correcting

　　Data Profiling

　　Data Profiling，其实目前还没找到非常恰当的翻译，Oracle里面用的是“数据概要分析”，但其实“Profiling”这个词用概要分析无法体现它的意境，看过美剧Criminal Minds(犯罪心理)的同学应该都知道FBI的犯罪行为分析小组(BAU)每集都会对罪犯做一个Criminal Profiling，以分析罪犯的身份背景、行为模式、心理状态等，所以Profiling更多的是一个剖析的过程。维基百科对Data Profiling的解释如下：

　　Data profiling is the process of examining the data available in an existing data source and collecting statistics and information about that data.

　　这里我们看到Data Profiling需要一个收集统计信息的过程(这也是犯罪心理中Garcia干的活)，那么如何让获取数据的统计信息呢?

　　熟悉数据库的同学应该知道数据库会对每张表做Analyze，一方面是为了让优化器可以选择合适的执行计划，另一方面对于一些查询可以直接使用分析得到的统计信息返回结果，比如COUNT(*)。这个其实就是简单的Data Profiling，Oracle数据仓库构建工具OWB中提供的Data Profiling的统计信息更加全面，针对建立Data Profile的表中的每个字段都有完整的统计信息，包括：

　　记录数、最大值、最小值、最大长度、最小长度、唯一值个数、NULL值个数、平均数和中位数，另外OWB还提供了six-sigma值，取值1-6，越高数据质量越好，当six-sigma的值为7的时候可以认为数据质量近乎是完美的。同时针对字段的唯一值，统计信息中给出了每个唯一值的分布频率，这个对发现一些异常数据是非常有用的，后面会详细介绍。

　　看到上面这些Data Profile的统计信息，我们可能会联想到统计学上面的统计描述，统计学上会使用一些统计量来描述一些数据集或者样本集的特征，如果我们没有类似OWB的这类ETL工具，我们同样可以借助统计学的这些知识来对数据进行简单的Profiling，这里不得不提一个非常实用的图表工具——箱形图(Box plot)，也叫箱线图、盒状图。我们可以尝试用箱形图来表现数据的分布特征：

　　箱线图有很多种表现形式，上面图中的是比较常见的一种箱线图。一般中间矩形箱的上下两边分别为数据集的上四分位数(75%，Q3)和下四分位数(25%，Q1)，中间的横线代表数据集的中位数(50%，Media，Q2)，同时有些箱线图会用“+”来表示数据集的均值。箱形的上下分别延伸出两条线，这两条线的末端(也叫“触须”)一般是距离箱形1.5个IQR(Q3-Q1，即箱形的长度)，所以上端的触须应该是Q3+1.5IQR，下端的触须是Q1-1.5IQR;如果数据集的最小值大于Q1-1.5IQR，我们就会使用最小值替换Q1-1.5IQR作为下方延伸线末端，同样如果最大值小于Q3+1.5IQR，用最大值作为上方延伸线的末端，如果最大或者最小值超出了Q1-1.5IQR到Q3+1.5IQR这个范围，我们将这些超出的数据称为离群点(Outlier)，在图中打印出来，即图中在上方触须之外的点。另外，有时候我们也会使用基于数据集的标准差σ，选择上下3σ的范围，或者使用置信水平为95%的置信区间来确定上下边界的末端值。

　　其实箱线图没有展现数据集的全貌，但通过对数据集几个关键统计量的图形化表现，可以让我们看清数据的整体分布和离散情况。

　　既然我们通过Data profiling已经可以得到如上的数据统计信息，那么如何利用这些统计信息来审核数据的质量，发现数据可能存在的异常和问题，并对数据进行有效的修正，或者清洗，进而得到“干净”的数据，这些内容就放到下一篇文章吧。

　　» 本文采用 BY-NC-SA 协议，转载请注明来源：网站数据分析 » 《分析的前提—数据质量1》

         原文链接：