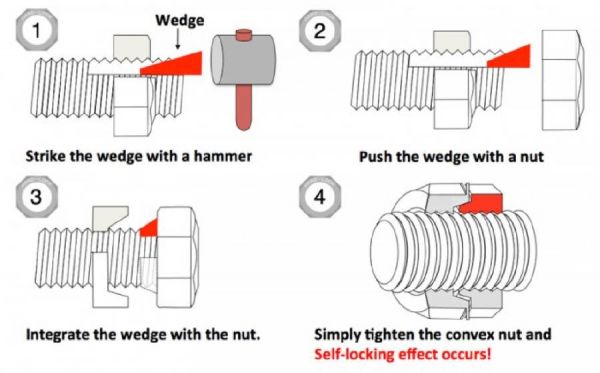
中国的高铁取得了令世界刮目相看的成绩，然而，小小的螺母却不得不采用进口的。因为高铁运营时，高速行驶的列车和铁轨不断接触，形成的震动非常大，一般的螺丝在这种震动中会被震松震飞，导致严重的交通事故。不想被震飞，就需要螺丝和螺母严丝合缝、永不松动才行。

　　这个要求看起来很简单，但是要满足它并不容易。大家想，世界上做螺丝螺母的企业可以说是多如牛毛，但是能生产这种永不松动螺母的企业有几家呢?只有一家，来自日本的哈德洛克工业株式会社。

　　让我们挖掘一下它的设计思路。原理很简单，在螺丝和螺母之间，打入一个梯形的楔子，可以起到牢固的效果。如果将螺母一分为二，再把其中一个螺母当作楔子使用，就可以起到加固作用。

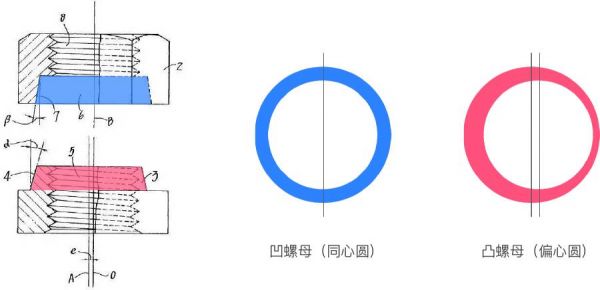
　　顺着思路，继续往下。左边是一分为二的螺母，上方我们叫凹螺母，采用了一个同心圆的设计，对应左图蓝色的部分。而下方我们叫它凸螺母，它采用了偏心圆的设计，对应左图红色的部分。可以看到，红色圆环的内外圆心并不在一条直线上。当我们把两个螺母拧到一起，也就是两个圆环重叠时，势必会产生错位。而螺母想要拧紧，就必须克服这种错位带来的巨大阻力。这种阻力，就是它永不松动的原因。

　　可能这样说还不够直观，我们把它们的关系想象成红酒瓶和软木塞，尺寸匹配的软木塞可以刚好打进瓶口里，并且轻松地拔出来。如果换成更大尺寸的软木塞(相当于错位的螺母)，就需要用更大的力气才能打进去，一旦打进去，再想拔出来也同样需要很大的力量。这种阻力带来的自紧力让它们彼此间很难松动，这就是几何的力量。

　　有的人可能会有疑惑，人家把这种螺母的原理和结构都明白地告诉你了，为什么还说能够生产这种螺母的只此一家。因为实际的生产还需要特殊的经验和技术。没有千万次试错的精神，就是琢磨透了原理，也无法仿制出同样的螺母。日本的很多企业都有这种怎样学也学不会的独一无二的技术。

　　斐波那契与兔子数列

　　讨论几何学设计，一定会提到的人就是斐波那契。这位意大利数学家提出过这样一道有趣的数学题：

　　问：兔子在出生两个月后，就具备繁殖能力，一对兔子每个月能生出一对小兔子。如果所有兔子都不死，那么一年以后可以繁殖多少对兔子?

　　起初，我们拥有一对兔子。

　　过了一个月，这对兔子还不具备繁殖能力，所以还是一对。

　　又过了一个月，这对兔子生了一对小兔子，现在有两对。

　　再过去一个月，老兔子继续生小兔子，而小兔子还不具备繁殖能力，所以有3对。

　　……以此类推。

　　一年后，我们一共有了233对兔子

　　我们发现，这个数列有一个共同的规律，两项之和可以得到后一项，这对任何一项都是成立的。最后，在数列最前面补一个0。

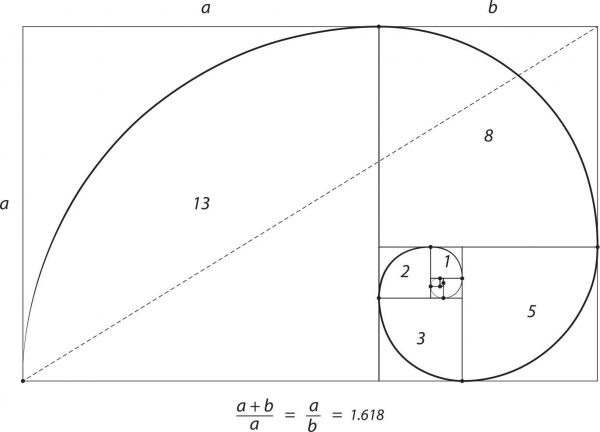
　　我们就得到了这样的一个数列，这个数列被称作斐波那契数列也叫黄金数列。大家可能都想到了黄金分割比、黄金螺旋线。那他们是如何产生联系的?让我们继续往下看。

　　取数列的末两位，求144和233的比值，我们得到的结果是0.618025751……

　　随着斐波那契数列项数的增加，前一项与后一项之比将越来越逼近黄金分割比(φ)，这也是为什么这个数列被称为黄金数列的原因。

　　在数学中，黄金分割比(φ)≈0.618033988749894848204586834…

　　它是一个小数点后无限不循环的无理数

　　如果我们把这一个个数，用正方形代替，会得到这样一个几何图形。当我们以正方形的边长为半径画圆，便会得出这条著名的黄金螺旋线。

　　这条线不是玄学，大家可能都知道，自然界很多生物上都能找到这根螺旋线，比如鹦鹉螺、向日葵等等，但未必很了解它们为什么会长成这样。

　　斐波那契与向日葵