|
“设计就是解决问题”——原研哉《设计中的设计》。交互设计作为一门融合计算机与心理学的设计学科,自然也是为解决问题而存在。交互设计旨在缩短实现模型与心理模型之间的鸿沟,同时通过最“优雅”的方式达成目标。所以说,交互设计就是一个求最优解的过程。 理性是基于现有的理论,通过合理的逻辑推导得到确定的结果。求解本身就是一个理性推导的过程,因此如何求解?如何求最优解?这些就是本文想探讨的地方。 本文目录提纲: 一、问题与解决问题 1、什么是问题? 2、怎么解决问题? 3、怎么选择一种最优方法? 二、交互设计与解决问题 1、怎样求得所有解 2、怎样推导最优解 三、总结 一、问题与解决问题 1、什么是问题? 问题是,造成应有状态(目标)与现有状态(现状)之间存在差距的各种影响因素就叫问题。把这些影响因素进行改变,就能解决问题,达成目标。
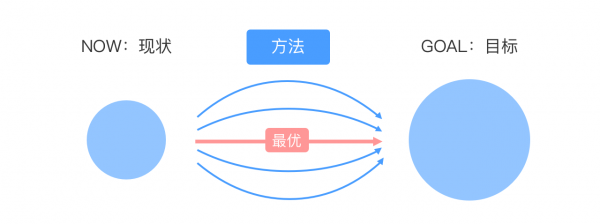
举一个例子:小明想吃汉堡包(目标),但是因为下雨没伞不能出门(现状),这就是问题。 2、怎么解决问题? 要实现目标,有很多很多种方式,这就是解决方法。
继续举例:小明想吃汉堡包,但是下雨没伞不能出门,他可以有其他方式吃到汉堡包。比如打电话叫外卖、打电话叫家人带回来…… 3、怎么选择一种最优方法 我们穷举的所有的方法都是可以达成目标的,但是在现实中我们只需要选择其中一个方法即可。因为我们只有一个目标。
继续举例小明:小明有多种方法可以实现吃汉堡的目标,但是只需要做一个决定即可。小明可以很随性,想到哪个就去采取。小明也可以很理性分析,做出最优选择。 小明会想很多因素:想最快吃到汉堡包(时间)。所以会从中选择其中一种解决方法:叫附近店铺的外卖。 所以整个过程思路:定义问题→穷举解→限制条件→最优解。 二、交互设计与解决问题 看完以上内容,有没有感觉似曾相识,交互设计同样是这样的过程: 从问题推导出所有的解(所有可能的情况),然后通过限制条件,得出最优解。
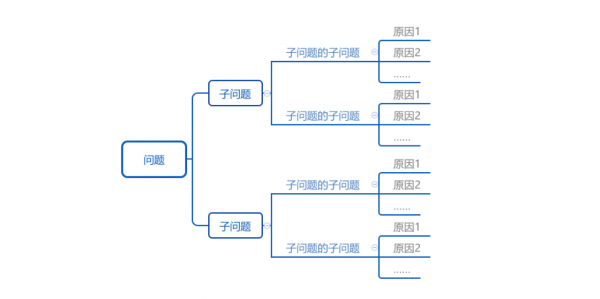
结合项目经验,我们都能知道:得到解不是难点,得出所有解、推导最优解才是最大难点。 1、怎么求得所有解? 解与问题本身有关。有些问题它的解只有一个,那么我们只需要给出肯定的答案即可;有些问题它的解有多个,那么我们就需要穷举。我们可以根据问题的不同类型,做出相应的解。 (1)问题类型一:“是非题” 也就是单一对立面问题。这类通常就是很具体的问题。正面不行,就取反面;同理,反面不行,就取正面。这类问题一般是“是否”、“有无”、“可否”…… 比如,现在遇到了一个问题,某个电商网站没有支持微信支付导致偏好微信支付用户无法支付。那么解决方法就是单一的,支持微信支付即可。它的解就是唯一的。 (2)问题类型二:“多因素问题” 这类问题是我们常见的问题,它是由多个因素导致的。因此解决方法也会多样。我们通常会先【拆解】这类问题,把它拆解到最后变成更单一的“是非题”。这类问题通常可以会借助思维导图来分析。
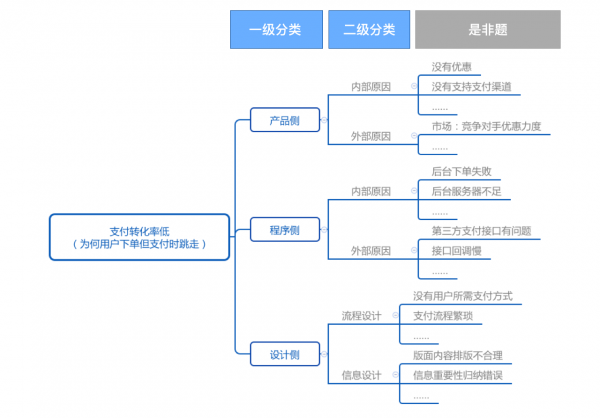
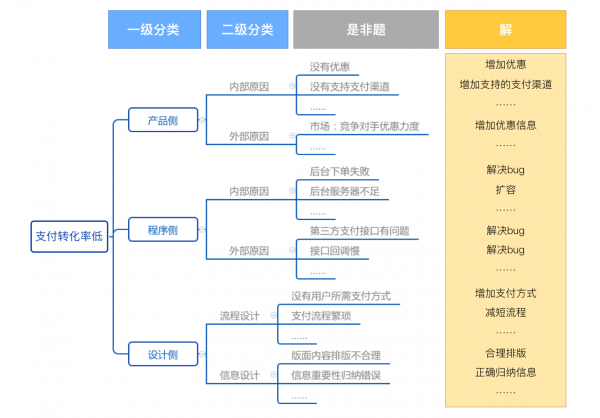
PS:在这里插入一个知识点,为了得到全面的解,分析过程中我们会用MECE的原则来穷举,即完全穷举、相互独立。为了达到MECE的目标,我们会引入三种逻辑结构:时间、结构、重要性。 时间:表示“时间先后”顺序,比如“过去、现在、未来”、“童年、青少年、中老年”等等 结构:表示“整体与部分”的逻辑关系,比如具体实物的构成、地理位置的构成、抽象概念的构成 重要性:表示“同类事物归为一类”的逻辑关系,这种是找到一类事物的共性特点,再按照共性特点体现的强弱组织论点的顺序。 举一个例子,现在产品遇到了一个问题,某个游戏的支付页面转化率比同期低了。那么我们要怎么解决问题? 首先,我们应该拆解问题,支付页面转化率低一定是多种原因的。首先要分一级原因,采用“结构逻辑”,可以分为产品、程序、设计。 其次,再可以把一级原因进行细分,一级原因还可以继续采取“结构逻辑”去拆解,比如内部原因、外部原因:
最后得到最基本的“是非题”,就可以穷尽所有的解。
(3)问题类型三,我们命名为“无穷解问题”。 (责任编辑:admin) |